Zur Statik trägerloser Abendkleider

Zur Diskussion statischer Probleme bei der Konstruktion trägerloser Abendkleider Inhaltsverzeichnis 1. Problemstellung 2. Diskussion der statischen Zusammen- hänge mit Lösungsansätzen 3. Zusammenfassung 4. Literaturhinweise 1. Problemstellung Das Problem ist uns allen hinreichend bekannt. Wer von uns Ingenieuren kann schon den Reizen einer attraktiven Kollegin widerstehen? Und wer von uns würde wegschauen, präsentierte sich doch diese Kollegin in einem aufregend gestylten trägerlosen Abendkleid? Doch, so wirkungsvoll ein trägerloses Abendkleid auch sein mag, wenn es gilt, die Aufmerksamkeit maskuliner Zeitgenossen zu erregen, so oft bereitet es seinem Statiker und Konstrukteur endloses Kopfzerbrechen. Denn er sieht sich dem Problem gegenüber, ein Kleidungsstück entwerfen zu müssen, welches so aussieht, als ob es jeden Moment zu Boden fallen könnte, dies jedoch mit einem, wenn auch nur kleinen, Sicherheitsfaktor nicht tut. Man kann es mithin erahnen. Ehe ein solches Kleid fertig geschneidert ist, sind eine Reihe von statischen Schwierigkeiten zu analysieren und zu bewältigen. In der nachfolgenden Analyse von trägerlosen Abend- kleidern werden die grundlegenden Zusammenhänge zu obigem Thema, welche bisher wissenschaftlich belegt werden konnten, verdeutlicht. 2. Diskussion der statischen Zusammenhänge und Lösungsansätze Für die Tatsache, daß das Kleid auch wirklich nicht fällt, gelten zunächst die uns allen wohlbekannten statischen Gleichgewichtsbedingungen. Betrachten wir zunächst einen infinitesimal kleinen Elementarstreifen aus Stoff an einem trägerlosen Abendkleid als freigeschnittenen Streifen im Bereich der Ebene A in Bild 1. Man kann sehen, daß die tangentialen Kräfte F1 und F2 wirken. Sie sind betragsmäßig gleich und heben sich daher gegeneinander auf. Die abwärts gerichtete Vertikalkraft W (bewirkt durch das Gewicht des Kleides) wird durch die Kraft V kompensiert, die senkrecht nach oben wirkt und von der Zugspannung im Stoff oberhalb der Ebene A stammt. Die algebraische Summe von jeweils vertikalen und horizontalen Kräften ergibt Null. Es wirken ferner keinerlei Drehmomente, womit die Gleichgewichtsbedingungen alle erfüllt sind, nämlich: ( SFx = 0 ; SFy = 0 ; SM = 0 ). Der Elementarstreifen befindet sich im Gleichge- wicht und ist folglich bewegungsfrei, so wie es in der Aufgabenstellung vom Konstrukteur verlangt wird. 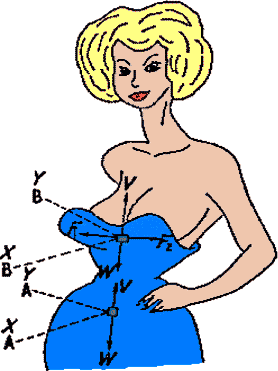Bild 1:  Die an den Kleidelementen angreifenden Kräfte Betrachten wir nun wiederum einen infintesimal kleinen Kleiderstreifen, der als freier Körper im Bereich der Ebene B des Bildes 1 isoliert wird. Die zwei Tangentialkräfte F1 und F2 sind entgegengesetzt gleich wie zuvor, doch die Kraft W (das Gewicht des Kleides) wird keineswegs durch eine aufwärtsgerichtete Kraft V kompensiert, da ja keinerlei Stoff oberhalb der Ebene B vorhanden ist, der diese Kraft liefern könnte. Daher ist zwar die algebraische Summe der horizontalen Kräfte gleich Null, die Summe der vertikalen Kräfte ist jedoch ungleich Null. Die Gleichgewichtsbedingungen werden in Ebene B also nur zum Teil erfüllt. Daher befindet sich dieser Elementarstreifen nicht im Gleichgewicht; ist folglich in Vertikalrichtung nicht bewegungsfrei. Aus gesellschaftlichen Gründen ist es jedoch zwingend notwendig, daß die Gleichgewichtsbe- dingungen für jeden denkbaren Elementarstreifen in jeder denkbaren Ebene grundsätzlich erfüllt sind. Gesetzt den Fall, die weibliche Person (Trägerin) wäre von Natur aus mit einer entsprechenden Oberweite gesegnet, so könnte sie diese äußerst notwendige Kraft mittels ausreichend großem Tragwerk selbst zur Verfügung stellen und den besagten Elementarstreifen, und damit auch das ganze Kleid, im Gleichgewicht erhalten. In den weitaus häufigeren Fällen jedoch müssen des Ingenieurs Erfahrung und Innovation bemühmt werden, um diese Kraft mit künstlichen Mitteln zu erzeugen. 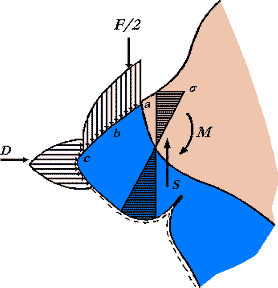Bild 2:  Kraftverteilung am Tragwerk (s = Biegespannung) In zahlreichen Fällen wird sich der Ingenieur die Reibungs- bzw. Haftungsgesetze zunütze machen, um diese Kraft zur Verfügung zu stellen. Die Haftungskraft ist durch die Formel: F = µ0 · N gegeben, in der F die Haftungskraft, µ0 den Haftungskoeffizienten und N die Normalkraft, die senkrecht auf F wirkt, darstellen. Da für ein vorgegebenes weibliches Wesen (dessen sekundären Geschlechtsmerkmalen) und ein vorgegebenes Abendkleid µ0 konstant ist, muß die Normalkraft N erhöht werden, wenn F vergrößert werden soll. Eine naheliegende Methode, die Normalkraft zu vergrößern, besteht darin, den Durchmesser des Kleidungsstückes in der Ebene in Höhe des Punktes C in Bild 2 kleiner als den Durchmesser der Trägerin in der gleichen Ebene zu wählen. Dies hat jedoch den Nachteil, daß die resultierende Kraft D aus der hier erzeugten Spannung durch den Punkt C geht und die Trägerin, falls der Durchmesser des Kleides zu gering gewählt wird, im Bereich des Tragwerks Unbehagen verspürt. Und dies verdeutlicht nun

Bild 3:  Beispielabb. den Konflikt zwischen der tragenden Damenwelt einerseits und den sich um alles in der Welt den Kopf zerbrechenden Ingenieu- ren andererseits, die nichts unversucht lassen, um allen Wünschen der nie zufriedenzustellenden weiblichen Zeitgenössinen gerecht zu werden. Dieser Konflikt wird auch durch folgenden Zusammenhang nocheinmal bestätigt: Bild 2 kann ebenfalls die Wirkung des Gewichtes W des Abendkleides als vertikale Streckenlast (parabolischer Verlauf *) auf dem Tragwerk entnommen werden. Da im Allgemeinen die Tragwerkskonstruktion aus zwei Traggestellen besteht (vereinfacht als zwei eingespannte Kragträger betrachtet) wirkt jeweils das halbe Gewicht als Resultierende vertikal durch den Punkt b. Als Schnittgrößen erhalten wir neben den Auflagerkräften auch das statisch bedeutsame Einspannmoment, welches sich zu M = F/2 · a - D · b ergibt, wobei a und b die zu den resultierenden Kräften zugehörigen Hebelarme sind, und von der individuellen Tragwerkskonstruktion abhängen. Die Formel verdeutlicht, daß das Einspann- moment, und damit die Biegespannung s an der Einspannstelle, mit wachsender Kraft D abnimmt (wir unterstellen hierbei, daß die meisten Tragwerke einen Hebelarm b > 0 zu Verfügung stellen). Für den Ingenieur gilt es nun einen Kompromiß zwischen dem bereits angesprochenen Durchmesser des Kleides und den zu erwartenden Schnittgrößen zu finden. Da nun das Gewicht des Kleides vom verwendeten Stoff abhängt, gilt auch die Formel W = r · V Für die Optimierung des Abendkleides gilt daher folgende Differentialgleichung: dD / dd + dW / dr = 0 Als ob das Problem noch nicht komplex genug wäre, fordern noch einige Damen, daß der Rückenausschnitt des Kleides tiefer verlegt wird, um die freie Oberfläche zu vergrößern und entsprechend mehr Aufmerksamkeit zu erregen. In diesem Falle wirken die Horizontalkräfte F1 und F2 aus Bild 1 nicht länger horizontal, sondern werden durch die Kräfte T1 und T2 ersetzt, die in einem Winkel a nach unten wirken. Daher besteht nun die gesamte abwärtsgerichtete Kraft aus dem Gewicht des Kleidungsstückes unterhalb von B, zuzüglich der Vektorsumme von T1 und T2. Diese vektorielle Summe nimmt in ihrer Größe zu, wenn der Rückenausschnitt vergrößert wird, da ja R = 2 · T · sin a gilt und der Winkel a mit zunehmendem Rücken- decolleté zunimmt. Daher muß die vertikal nach oben wirkende Kraft vergrößert werden, die für das Gleichgewicht notwendig ist, wenn Abendkleider mit tiefem Rückenausschnitt gewünscht werden. Fairerweise sein hierbei noch erwähnt, daß die Vergrößerung des Rückenausschnittes zur Verminderung des Eigengewichtes des Kleides infolge Stoffeinsparung beiträgt, jedoch kann auch gesagt werden, daß dieser dem Ingenieur entgegenkommende Umstand nur geringen Einfluß auf die Gesamtstatik des Kleides ausübt. Es ist hinlänglich bekannt, daß Abendkleider auch zu oder gerade bei Tanzveranstaltungen getragen werden. Folglich wirkt hin und wieder eine zufällige horizontale Kraft, welche in Bild 2 zusätzlich zur Kraft D auf das Tragwerk im Punkte C, wobei diese stoßartige Belastung alle Kraftlinien in diesem Punkte zusammenfallen läßt. Dies führt zu einem Verschwinden der Spannung in den Kraftlinien zwischen a und b, jedoch wird die Kompression in der Ebene durch c erhöht. Die kritische Fläche befindet sich in der Einspannstelle, da hier die Kraftlinien nicht nur einer Kompression aufgrund Kraftmoment und Stoß unterliegen, sondern auch noch einer Sicherungskraft S. Sollte ein langes schweres Kleid einer derartigen Stoßbelastung ausgesetzt sein, können die Kraftlinien im Auflagerbereich bis an den "Gefahrenpunkt" gebracht werden. 3. Zusammenfassung Besonders der zuletzt erwähnte Zusammenhang zwischen Stoßbelastung und Spannungsabfall im Auflagerbereich dürfte jedoch ohne umfassende experimentelle Untersuchungen, also nur aufgrund von theoretischen überlegungen nicht eindeutig mathematisch zu beschreiben sein. Demzufolge dürften dieses Phänomen sowie weitergehende Probleme, wie z.B. das Verhalten des Kleides unter Berücksichtigung der beim Tanzen einsetzenden Schwingungen und Rotationsbeschleunigungen, bedauerlicherweise nicht experimentell bestimmbar, geschweige denn nachweisbar sein. Dies dürfte weniger auf den Mangel an geeigneten Tragwerken, denn an der Bereitschaft von geeigneten Versuchspersonen für experimentelle Untersuchungen zurückzuführen sein. Viele weibliche Zeitgenössinen wurden gebeten, sich für Experimente auf der Grundlage dieser Untersuchung im Interesse der Wissenschaft (und letztlich auch in ihrem eigenen Interesse) zur Verfügung zu stellen, jedoch kam bis dato aus noch unerklärlichen Gründen keine ensthafte Zusammenarbeit zustande. Dieser Umstand ist umsomehr bedauerlich je mehr die Wissenschaft die Erkenntnis gewinnt, daß die weiblichen Tragwerke (naturbedingt) sich unter Belastung eben nicht exakt nach der bernoullischen Biegetheorie verformen ("...ebene Querschnitte bleiben nach der Verformung eben..."). Man kann hier schon erkennen, daß der Einfluß der Tragwerksverformung auf die Konstruktion eines individuell angefertigten trägerlosen Abendkleids nur mittels EDV und hohen Rechenaufwandes nach der Finite- Elemente-Methode berechenbar sein dürfte. Andererseits besteht auch für den Forscher die Schwierigkeit, beim Anblick der zu untersuchenden Tragwerke seine Gedanken beisamenzuhalten und sich nur auf die rein wissenschaftlichen Fakten zu konzentrieren. Daher wird man bis auf weiteres wohl Versuch und Irrtum und scharf- sinnige Vermutungen als Grundlage zum Entwurf trägerloser Abendkleider gelten lassen müssen, bis eines Tages gründliche Untersuchungen gemacht werden können. 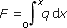- - - - - - - - - - - - - - - - - - - - - - - - * Da die Tragwerke unterschiedlichster Natur sein können, gilt für die resultierende Kraft F streng genommen die Formel: In den weitaus häufigsten Fällen dürfte jedoch näherungsweise die mathematischen Beschrei- bung mittels eines parabolischen Ansatzes hinreichend genaue Ergebnisse liefern. 4. Literaturhinweise (powered by Pepilog) Oliver Romberg: Keine Panik vor Mechanik! Dietmar Gross: Technische Mechanik 1. Statik Helga Dankert: Technische Mechanik. Statik, Festigkeitslehre, Kinematik / Kinetik Alfred Böge: Formeln und Tabellen zur Technischen Mechanik Dietmar Gross: Aufgaben zu Technische Mechanik 1 - 3. Statik, Elastostatik, Kinetik Dietmar Gross: Formeln und Aufgaben zur Technischen Mechanik 1. Statik Hans A. Richard: Technische Mechanik - Statik Hirschfeld: Baustatik, 3. Auflage Hobitz: Verformungsverhalten weicher Tragwerke, Dissertation am Institut für Biostatik, Deutsche Hochschule für Verbundfaser- forschung, München (DHV-M) München, 1986 © Elias Tzimogiannis