 |
 Problem: Viele physikalische Funktionen hängen von zwei Parametern ab. Der Zusammenhang wird dann oft mittels diskreter Wertetabellen beschrieben. Diese Wertematrix kann man sich wie ein das Problem beschreibendes Gitter vorstellen. Braucht man nun einen Wert der nicht in der Wertetabelle enthalten ist, so muß man in zwei Dimensionen interpolieren. Die Stützstellen für die Interpolation bilden die vier nächsten beim gesuchten Wert liegenden Werte (Gitterpunkte). |
|
Beispiel: Die optimale Geschwindigkeit eines Flugzeugs hängt von seinem Gewicht und der Flughöhe ab.
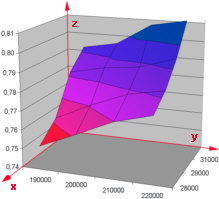
Das Beispiel rechts zeigt die Long-Range-Cruise Machzahl (z-Achse) einer Boeing 747-400 in Abhängigkeit des Gewichts (y-Achse in kg) und der Flughöhe (x-Achse in ft). Definiert ist der Zusammenhang über eine 2-dimensionale Wertetabelle: Machzahl = f (Flughöhe,Gewicht).
Muß der Pilot nun auf Flightlevel 300 (30000 ft) fliegen und das Flugzeug wiegt aktuell 214 Tonnen, so kann er die optimale Machzahl nicht auf Anhieb ablesen. Er muß interpolieren. Als Stützstellen nimmt man die benachbarten gegebenen vier Wertepaare. (Beispielwerte eintragen) |
 |
|
|
|
|
|
Hinweise: Interpoliert wird (es geht auch gar nicht anders) immer linear. Dezimaltrennzeichen ist der Punkt. Die Stützstellen dürfen nicht deckungsgleich sein. Auch Extrapolationen sind möglich. Fragen? |
