Winddreieck (E6B)

	Zeichnerische Konstruktion des Winddreiecks
	Nordrichtung einzeichnen (TN), danach den Kurs einzeichnen (beginnend bei TN im Uhrzeigersinn) Kursvektor beschriften mit  "TC / GS" am Ende des Kursvektors den Wind so antragen, dass die Windpfeilspitze zur Kursvektorspitze zeigt, Windvektor beschriften mit  "W / V" einen Maßstab wählen (z.B. 1 cm = 1 kt) und den Betrag der Windgeschwindigkeit am Windvektor abtragen mit dem Zirkel am Ende des Windvektors ein- stechen und einen Kreisbogen am Kursvektor abtragen, Radius ist die Eigengeschwindigkeit TAS Einstechpunkt und Schnittpunkt Kreisbogen / Kursvektor verbinden, den sich ergebenden "Steuerkurs"-Vektor bezeichnen mit TH / TAS
	Die Länge des entstandenen Vektors (TC / GS) entspricht der Grundgeschwindigkeit, der Winkel zwischen dem Steuer und dem Grundkurs ist der Vorhaltewinkel bzw die Abdrift, alle weiteren Winkel wie Windwinkel oder Windeinfallswinkel sind ebenfalls abzulesen.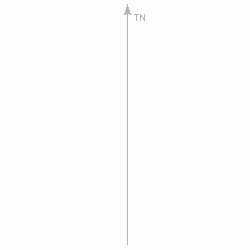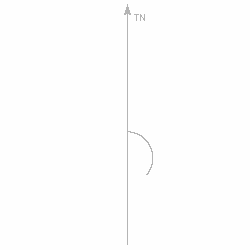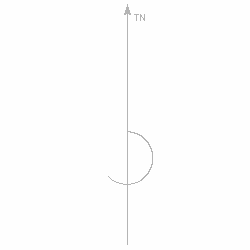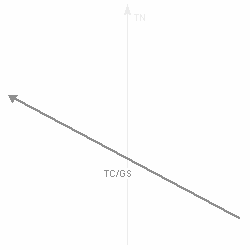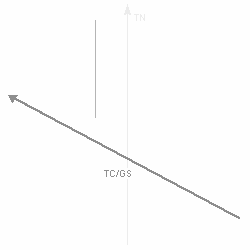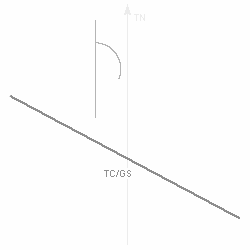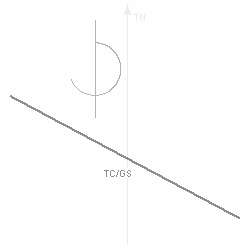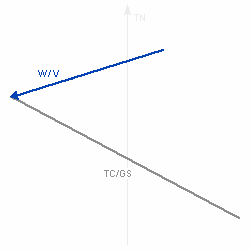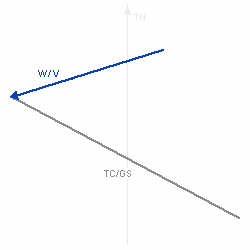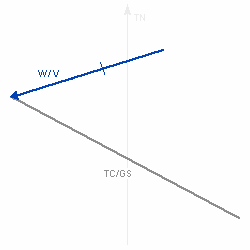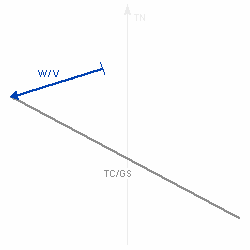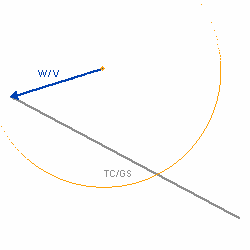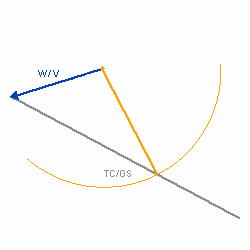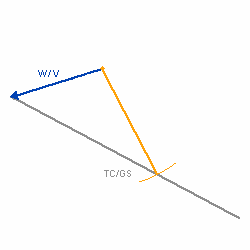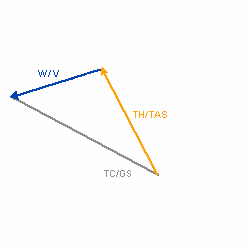

	Mathematische Grundlage
	Die mathematische Grundlage für das Winddreieck ist der Sinussatz. Durch simples umstellen läßt sich alles berechnen was von Interesse ist:     WS / sin(WCA)   =   TAS / sin(WA)   =   GS / sin(WA-WCA)

	Verwendung eines sog. Drehmeiers
	Eine weitere Möglichkeit an die begehrten Informationen zu kommen ist die Nutzung eines Navigations- rechners. Die Nutzung ist denkbar einfach und meist auf dem Gerät selbst aufgedruckt.
	Scheibe drehen bis Windrichtung unter dem "True Index" steht Auf der Scheibe mit Hilfe eines Filzstiftes und des darunterliegenden Rasters die Windgeschwindigkeit abtragen (Bsp. 15 kt Wind: Drehpunkt auf 160 und weiter oben bei 175 einen Punkt antragen Scheibe drehen bis der rechtweisende Kurs unter dem "True Index" steht Scheibe vertikal verschieben bis der selbst markierte Punkt über der geplanten TAS zum liegen kommt (z.B. 110 Linie) Ergebnis: Die Grundgeschwindigkeit (GS) kann unter dem Drehpunkt (center) abgelesen werden Ergebnis: Der Vorhaltewinkel (WCA) ist der Winkel zwischen der Mittellinie und dem selbst markierten Punkt. Ist der Punkt links von der Mittellinie, so bedeutet dies links vorhalten.
	Ein Vorteil dieses mechanischen Rechenschiebers ist, das der einmal abgetragene Wind immer wieder für weitere Berechnungen genutzt werden kann. Außerdem sind diese Rechenhilfen relativ preiswert und robust. Nachteil ist die unflexible Fixierung auf ein Aufgaben-Schema sowie die endliche Genauigkeit. Tip: Zwei richtig gute interaktive Drehmeier gibt es hier in Flash realisiert und hier als Java-Applett.